Les marées
Genèse des marées
Rôle de la lune

La terre subit l'attraction de la lune (et vice-versa). Cette attraction est proportionnelle à la masse de la lune et inversement proportionnelle au carré de la distance. De plus, la terre et la lune constituent un système en mouvement de rotation. En raison de la faible masse de la lune, le centre de rotation est proche du centre de la terre, c'est pourquoi on dit que la lune tourne autour de la terre, ce qui est presque vrai.
Il résulte de cela un déplacement des masses hydriques en faveur de l'axe terre - lune au détriment du reste de la surface de la terre. En ces zones, la mer est haute. Dans les zones proches du plan orthogonal à cet axe, elle est basse. La terre change d'orientation dans ce système, si bien qu'en un point donné, la marée monte ou descend.
Rôle du soleil
Le soleil joue le même rôle mais dans des proportions bien moindres. Sa masse est certes considérable, mais le carré de la distance soleil terre est considérablement plus élevé. Son action ne fait qu'infléchir celle de la lune.
- Lorsque le soleil est dans l'axe terre-lune (quel que soit le côté), il renforce les marées. On est alors en vives eaux. (1 et 2)
- Lorsque le soleil est dans un axe orthogonal, il diminue cette action. Ce sont des mortes eaux. (3)

Calcul de marées
Vocabulaire
- On appelle flot la marée montante et jusant la marée descendante.
- Les grandes marées sont aussi appelées vives eaux. La mer monte plus haut et descend plus bas. Le coefficient de marée approche 120.
- Lors des mortes eaux, la mer descend peu et monte peu. Le coefficient approche 60.
- La marée haute est appelée pleine mer (PM), la marée basse basse mer (BM).
- La différence de hauteur entre BM et PM s'appelle le marnage (c'est une mesure verticale). Il est en rapport avec le coefficient de marée.
- L'estran est la zone découverte en BM et recouverte en PM (c'est une mesure quasiment horizontale). L'estran est d'autant plus élevé que le coefficient de marées est élevé, mais surtout que le sol est plat.
- On dit couramment que la mer est étale ½ heure avant et après l'inversion de marée. Ce n'est qu'une impression liée à la faible vitesse du mouvement. L'étale n'existe théoriquement pas.
Règle des douzièmes
Chaque marée (flot ou jusant) dure approximativement 6 heures 1/4. Pour simplifier le calcul, on divise cette période en 6 "heures marée" de durée identique (souvent 1 heure et 2,5 minutes).
Remarque pratique : en France, une marée dure 6h15, donc 4 marées durent 25 heures ; c'est pourquoi les marées se reproduisent de jour en jour avec une retard de 1 heure par jour.
- Pendant la 1° et la 6° heure, la mer parcourt 1/12 de son trajet.
- Pendant la 2° et la 5° heure, la mer parcourt 2/12 de son trajet.
- Pendant la 3° et la 4° heure, la mer parcourt 3/12 de son trajet.
Si on représentait la hauteur d'eau en un point pendant un flot et un jusant, la courbe aurait l'allure suivante :
En ordonnées : la hauteur graduée en douzièmes du marnage
En abscisses : le temps en heures marée.
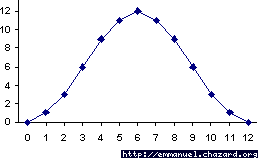
Calcul de hauteur d'eau en pratique
Cette section explique comment réaliser un graphe qui permet, à partir des indications d'un calendrier des marées, d'interpoler la hauteur d'eau à une heure précisée. Un calendrier des marées donnera :
- Le coefficient (nombre généralement compris entre 60 et 120). Sa valeur n'entre pas en compte dans la méthode de calcul.
- L'heure de la marée basse et de la marée haute dans un port de référence (des corrections numériques sont disponibles pour les autres ports).
- Les hauteurs d'eau en haute mer et basse mer. La hauteur 0 est la hauteur des plus basses mers. C'est la hauteur d'eau à marée basse lorsque le coefficient est de 120. C'est sur la base de cette hauteur d'eau que sont calculées les profondeurs affichées sur les cartes marines. (Il existe là aussi une correction selon les ports).
Soit l'exemple suivant, au mois de juillet :
| Horaire | Hauteur | |
| BM | 03h30 | 1m30 |
| PM | 09h42 | 3m50 |
Attention : les heures sont souvent données en UT (temps universel). Aussi faut-il ajouter 2 heures en été, et 1 heure en hiver pour compenser le décalage horaire.
Ainsi notre exemple devient-il :
| Horaire | Hauteur | |
| BM | 05h30 | 1m30 |
| PM | 11h42 | 3m50 |
où PM signifie pleine mer et BM signifie basse mer.
Il faut d'abord calculer la durée d'un heure marée :
[(11h42) - (05h30)] / 6 = 1h02
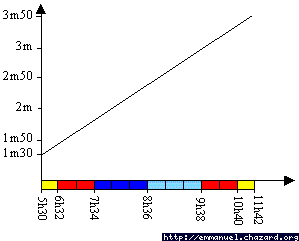
On représente sur le graphique :
- en ordonnées la hauteur d'eau, graduation régulière.
- en abscisses le temps, gradué avec les intervalles suivants : 1, 2, 3, 3, 2, 1. Cette échelle compensée permet de transformer la courbe en droite.
Il suffit de placer les points de PM et BM et de les relier. On peut lire la hauteur d'eau à une heure donnée et inversement ; avec la précaution suivante : l'échelle des abscisses n'est pas proportionnelle.
D'autres types de marées
En réalité, ce qui précède est valable en Europe, mais il n'en est pas de même du monde entier. Le dessin ci-dessous vous montre 4 types de marées.

Lecture de cartes : profondeur et courants
Les hauteurs d'eau indiquées sur les cartes sont les plus basses hauteurs : elles correspondent à une BM de coefficient 120. Pour avoir la hauteur d'eau, il faut ajouter au nombre lu sur la carte la hauteur calculée grâce au graphique précédemment établi. Pour information seulement, autant les mesures de profondeur s'appuient sur une BM de coefficient 120, autant les altitudes des points émergés (collines, amers, points d'intérêt) sont calculées par référence à la hauteur moyenne des eaux, en milieu de marée.
Les cartes marines renseignent aussi sur les courants. Ils sont parfois écrits directement, en particulier dans les golfes ou archipels : cela permet de connaître leur vitesse moyenne, et également leur sens, qui n'est pas toujours évident à deviner. Notez que la vitesse du courant n'est pas nécessairement la même en valeur absolue au flot et au jusant.
Cependant, en règle générale, quelques principes simples suffisent :
- le courant est plus fort en milieu de marée (3° et 4° heures)
- le courant emprunte habituellement le sens le plus logique, selon que la mer monte ou descend
- le courant est d'autant plus fort que le coefficient de marée est élevé, que le marnage est important
- dans les golfes et les archipels, les couloirs sous marins (zones plus profondes) sont des endroits où les courants seront les plus forts
- dans les golfes et les archipels, si un détroit est un passage obligé, le courant y sera d'autant plus fort qu'il sera étroit et que le volume d'eau drainée sera important.
Enfin, il est surprenant d'observer que parfois, au plus près des rochers, existent des contrecourants de sens opposé au sens normal. Cela peut être pratique pour les catamarans, dont le tirant d'eau est très faible.